ВЛИЯНИЕ ХАРАКТЕРИСТИК РЕАЛЬНОГО АВТОПИЛОТА. НА ДИНАМИКУ ПОЛЕТА В ТУРБУЛЕНТНОЙ АТМОСФЕРЕ

В § 2.2 при рассмотрении уравнений автопилота было огово­рено, что принятые для анализа законы управления описывают идеальные автопилоты. «Идеальность» этих автопилотов заклю­чается в том, что при анализе динамики системы самолет — ав­топилот не учитываются запаздывания автопилота и нелинейно­сти в его характеристиках. Современные автопилоты имеют достаточно хорошие технические характеристики, и их запаздыва­ние и различные нелинейности обычно не оказывают существен­ного влияния на динамические свойства системы самолет — ав­топилот в режиме стабилизации угловых координат.

В данном параграфе оцени­вается влияние указанных осо­бенностей реальных автопилотов на динамику полета в турбулент­ной атмосфере с целью обоснова­ния возможности использования в этом случае уравнений идеаль­ных автопилотов.

Рассмотрим влияние следующих характеристик реальных ав­топилотов:

1) времени запаздывания:

2) зоны нечувствительности;

3) ограничения угла отклонения руля.

Анализ проведем для автопилотов с жесткой обратной связью, поскольку именно этот тип автопилотов получил в настоящее вре­мя преимущественное распространение.

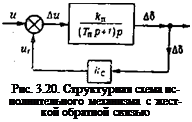
Основным источником запаздывания автопилота обычно яв­ляется его исполнительный механизм (привод рулевого органа). Структурная схема исполнительного механизма автопилота с жесткой обратной связью показана на рис. 3.20.

На этом рисунке обозначено:

и — сигнал, поступающий на исполнительный механизм с чувствительного элемента или счетно-решающего уст­ройства автопилота;

Д6 — угол отклонения руля;

щ — сигнал обратной связи, поступающий по этой цепи с ко­эффициентом kc;

k„ — коэффициент усиления исполнительного механизма, равный отношению угловой скорости руля и напряже­ния Ди на входе;

Тп — постоянная времени исполнительного механизма.

Структурная схема исполнительного механизма, показанная на рис. 3.20, справедлива для электрических, гидравлических и

пневматических рулевых машин. На основании этой структурной схемы получаем дифференциальное уравнение, описывающее ди­намику исполнительного механизма автопилота:

Т„ dm.________________ 1_ . Л£ = _J_

fc„kc dt* ‘ fc„kc dt kc

Исполнительные механизмы автопилотов конструируются так, чтобы постоянная времени Тп была как можно меньше (практи­чески сотые доли секунды). Эта постоянная делится на произ­ведение коэффициентов &П&С, которое обычно лежит в пределах 3—10 сект1. По указанным причинам коэффициент при второй производной оказывается очень малым, и этим членом можно пренебречь. В результате из (3.35) получаем уравнение инерци­онного звена

‘Л,-^ + д8=‘>, (3.36)

где Ta = jfc„fcc—постоянная времени исполнительного меха­низма;

ia= 1/Ас—передаточное число исполнительного меха­низма.

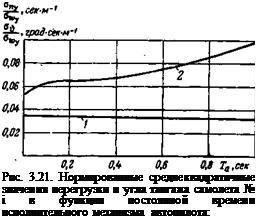
Значение постоянной времени Та у современных автопилотов равно 0,1—0,3 сек, и она в основном определяет запаздывание ав­топилота. Время затухания короткопериодического движения у со­временных самолетов с автопилотом колеблется в пределах 3— 10 сек (см., например, рис. 3.17,6 и 3.18,6). Поэтому можно ут­верждать, что запаздывание автопилота не должно сколько-ни­будь значительно влиять на динамику системы самолет — автопи­лот. Для проверки этого утверждения при условиях полета в тур­булентной атмосфере на рис. 3.21 приведена зависимость средне­квадратичных значений перегрузки (кривая /) и угла тангажа (кривая 2) для самолета № 1 в функции запаздывания автопилота Та. Масштаб турбулентности L равен 500 м. Графики на этом ри­сунке показывают, что с увеличением постоянной времени авто­пилота, т. е. его запаздывания, колебания по тангажу увеличива­ются, а перегрузка незначительно уменьшается. При этом посто­янная времени изменялась от 0 до значения 70=1 сек, которое не встречается в реальных автопилотах.

Снижение перегрузки при увеличении запаздывания автопило­та объясняется тем, что при этом ухудшается стабилизация угла тангажа и несколько увеличивается положительная роль момен­та статической устойчивости. Однако использование этого эффек­та путем искусственного увеличения запаздывания автопилота при полете в возмущенной атмосфере нецелесообразно, так как снижение перегрузки оказывается ничтожным.

На основании изложенного можно утверждать, что время за­паздывания реальных автопилотов не оказывает сколько-нибудь заметного влияния на наиболее существенный параметр движе-
ния саімолета в турбулентной атмосфере — вертикальную пере­грузку.

Перейдем к анализу влияния зоны нечувствительности на ха­рактеристики автопилота при полете в турбулентной атмосфере. На рис. 3.22 показана характеристика автопилота с зоной нечув­ствительности. На этом рисунке обозначено:

2а — ширина зоны нечувствительности;

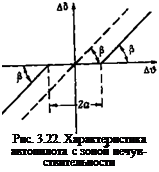Р — угол наклона линейного участка характеристики (тангенс этого угла равен передаточному числу автопилота). Пунктирная прямая, проходящая через начало координат, является характе­ристикой идеального автопилота (без зоны нечувствительности).

/ — перегрузка; 2 — угол тангажа

При случайных колебаниях угла тангажа под действием по­рывов ветра угол отклонения руля будет также случайной функ­цией. Связь между этими величинами определяется нелинейной характеристикой, показанной на рис. 3.22.

Для нелинейных систем связь между вероятностными харак­теристиками возмущающего воздействия и каким-либо выходным параметром в общем виде не выражается в аналитической форме. Однако в приближенной форме такую связь можно найти, если использовать метод статистической линеаризации нелинейностей. Основная идея этого метода состоит в аппроксимации нелиней­ной характеристики линеаризованной зависимостью между слу­чайными функциями, статистически эквивалентной этой харак­теристике.

Задача статистической линеаризации решена в работе [36] для безынерционных нелинейных элементов с самыми различны­ми характеристиками. На основании [36] нелинейная характери­стика рис. 3.22 при случайном стационарном характере измене-

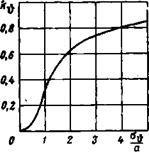
лом, определяемый табл. D. 1 (см. «Приложе­ние D»). Зависимость k» от а* /а представлена на рис. 3.23. Этот гра­фик показывает, что за счет линеаризующего влияния колебаний угла тангажа зона нечувствительности в характеристике автопилота сглажи­вается. Каждому среднеквадратичному значению угла тангажа соответствует свое передаточное число автопилота, определяемое на основании (3.38). При небольших среднеквадратич­ных значениях угла тангажа зона не­чувствительности существенно умень­шает передаточное число автопилота, что необходимо принимать во внима­ние при расчетах. В практически наи­более важном случае интенсивной тур­булентности, когда среднеквадратич­ные значения угла тангажа значитель­но превосходят половину зоны нечувствительности, коэффициент k ь близок к единице, и зону нечувствительности автопилота мож­но не учитывать. Абсолютное значение зоны нечувствительности по угловым ко­ординатам у различных современных автопилотов отличается не­значительно. У автопилотов, используемых в настоящее время, значения зоны нечувствительности по всем трем каналам (тан­гаж, крен, рыскание) лежат в пределах 0,2—0,5°. Приведенная выше методика учета зоны нечувствительности автопилота по угловым координатам может быть применена и для оценки влияния зоны нечувствительности в характеристиках автопилота по линейным координатам и по угловым скоростям. Необходимо заметить, что передаточное число линеаризован­ного автопилота с зоной нечувствительности зависит от значения неизвестного входного сигнала, воздействующего на нелинейный

Рис. 3.23. Коэффициент ста­тистической линеаризации

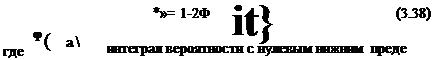элемент параметра системы, например, среднеквадратического значения угла тангажа, зависящего в свою очередь от передаточ­ного числа. По этой причине решение задачи о движении самоле­та при учете зоны нечувствительности должно производиться методом последовательных приближений. Ввиду громоздкости метода его применение практически возможно только на вычис­лительных машинах.

Рассмотрим влияние ограничения угла отклонения руля на ра­боту автопилота при полете в турбулентной атмосфере. Отклоне­ние рулей при управлении полетом с помощью автопилота ограничивается весьма существенно по сравнению с отклонением, которое может сделать летчик с помощью штурвала или педалей.

высоты вверх на 25° и вниз на 15°. Полный же диапазон переме­щения руля высоты с помощью автопилота составляет всего 6°, т. е. ±3°. Ограничение отклонения рулей с помощью автопилота диктуется необходимостью обеспечить безопасность полета при выходе автопилота из строя.

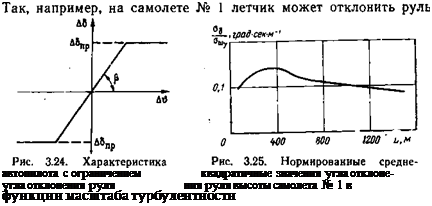
Характеристика автопилота с учетом указанного ограничения (без зоны нечувствительности) показана на рис. 3.24. Чтобы оце­нить влияние этого ограничения на динамику полета в турбулент­ной атмосфере, определим, насколько отклоняется руль при раз­личных скоростях ветра. На рис. 3.25 представлена зависимость среднеквадратичного значения угла отклонения руля высоты са­молета № 1 в функции масштаба турбулентности L. Наибольшее среднеквадратичное значение угла отклонения руля на единицу среднеквадратичного значения скорости ветра на рис. 3.25 равно 0,135. Даже в грозовых условиях вероятность попадания в об­ласть с аю=5 м/сек ничтожно мала. При <Ти.=5 м/сек среднеквад­ратичное значение угла отклонения руля составит 0,675°. На ос — — новании «правила За» можно утверждать*, что максимальное значение угла отклонения руля у самолета № 1 с вероятностью

См. «приложение D», стр. 244.

0,997 не превысит значения Абт=2,025°. Таким образом, руль вы­соты на самолете № 1 при полете в турбулентной атмосфере да­же при а, г=5 м/сек не дойдет до ограничений, и при анализе ди­намики системы самолет— автопилот в этих условиях можно не учитывать ограничение угла отклонения руля высоты.

Хотя этот вывод получен по данным конкретного самолета, он имеет достаточно общий характер, поскольку ограничение уг­лов отклонения рулевых органов при использовании автопилота для всех самолетов выбирается на основании одного и того же критерия безопасности. Кроме того, если характеристики самоле­та и автопилота известны, то этот вывод может быть проверен по приведенной выше методике. Полученные результаты дают возможность при анализе динамики самолета в турбулентной ат­мосфере не учитывать ограничений отклонения руля высоты, если закон управления автопилота имеет обычный вид.

Когда самолетом в аналогичных условиях управляет летчик, углы отклонения руля будут значительно больше. Летчик не успе­вает во время отклонить руль для стабилизации самолета в усло­виях болтанки, отклонения угловых координат быстро накапли­ваются, и для их ликвидации приходится давать большие откло­нения руля.